Free Space Detection¶

The “free space” is defined as the ensemble of grid points that do not overlap any atom. The free space detection algorithm is very straightforward. A grid with with mesh size grid_spacing is defined within the Maximum Englobing Region. Each grid point is then set to OFF if it overlaps an atom. In terms of pseudo-code, it could be expressed as:

Initialize MER
FreeSpace = MER[GridPoints]
FOREACH Atom IN SetOfAllAtoms:
    Points = MER[GridPoints] WITHIN Atom[radius] OF Atom
    FreeSpace = FreeSpace - Points

Non-contiguous Points Removal¶

Due to the intrinsic properties of the algorithm described above, many points can be detected as “free space” while being separated from the actual pocket by several Å.

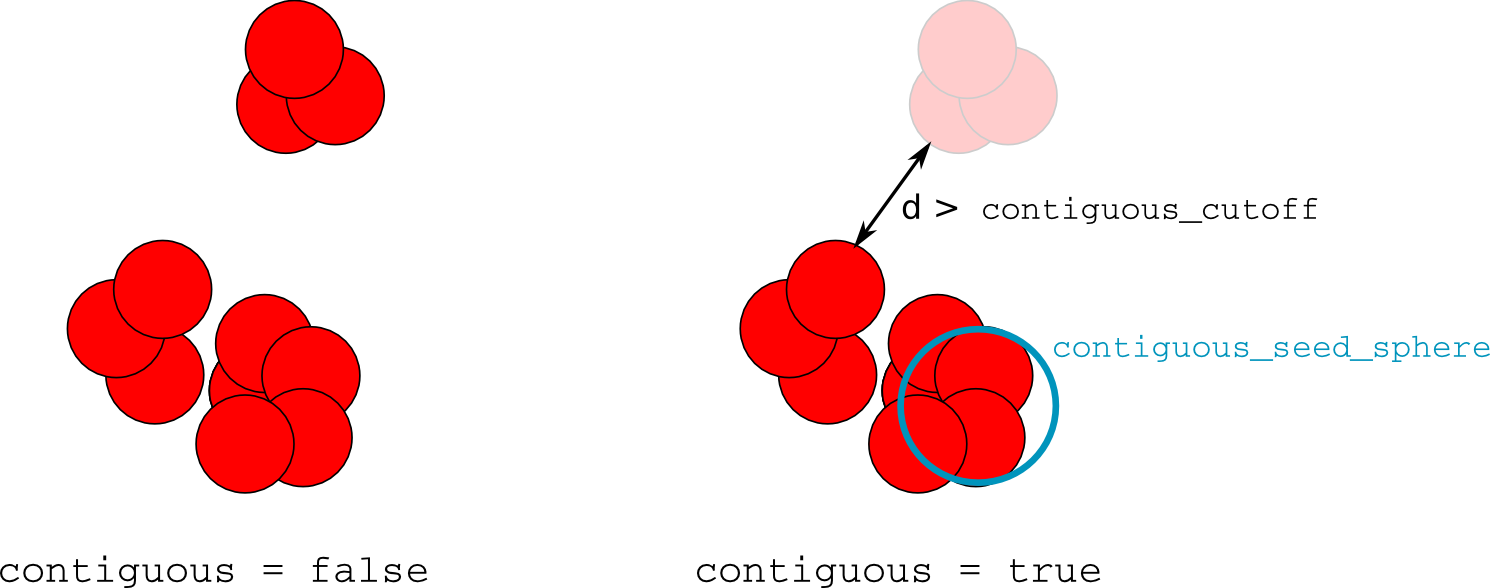
Which free space points are removed by contiguous points removal algorithm. On the left panel, no point detected as free space is removed, as the contiguous parameter is set to false. On the right panel, the contiguous is set to true and a contiguous seed region has been defined. Non-contiguous points are points that are neither within the contiguous seed region, neither within contiguous_cutoff of any atom detected as contiguous.

This algorithm allows to eliminate these points by iteratively redefining FreeSpacePoints as those that are within the contiguous_seed_region or within contiguous_cutoff of any point in the seed region.

Seed = [points IN FreeSpace AND IN SeedRegion]
Initialize Points IN Seed TO visited
WHILE Seed IS NOT EMPTY:
    Point = Seed[0]
    Neighbors = [Points OF FreeSpace WITHIN contiguous_cutoff OF Point]
    FOREACH N IN Neighbors:
        IF N IS IN FreeSpace AND IS NOT visited:
            Set N TO visited
            Add N TO Seed
FreeSpace = [points IF visited]

Volume Calculation¶

The exact value for the volume of the free space previously detected can be very tricky to calculate. Epock uses a thin grid defined in the limits of the free space (the mesh size MeshSize of this grid is 1/precision). The algorithm used for Free Space Detection can be used again to detect grid points that overlap FreeSpacePoints. The pocket volume 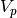is then

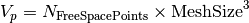
Pore Profile¶

The calculation of the pore profile is done by determining, for each z-level of the grid, which point (among those previously flagged as “free space”) is the farthest away from any points on the free space’ surface.

In mathematical terms, this can be expressed as 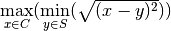, 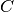being the set of free space points, and 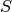the surface points.

The algorithm can be expressed as:

FOREACH level IN gridLevels:
    Initialize min[level] TO Infinity
    FOREACH point IN FreeSpace[level]:
        Initialize current_min TO Infinity
        FOREACH surface_point IN FreeSpace[level][surface_points]:
            IF distance(point, surface_point) < current_rmin:
                current_rmin = distance(point, surface_point)
        IF current_min < min[level]:
            center[level] = point
            min[level] = current_min

For any z value of the grid for which no center points has been found, the radius is set to 0.

The algorithm above will fail to give reasonable results when more than one cavity is detected. This is especially problematic when a very small secondary cavity is detected, for example a slight gap inbetween two side chains. This can be avoided by adding contiguous = true (see Non-contiguous Points).

Important Note. As pore radius is calculated on the free space points previously detected, it is important to get free space detected, even in narrow regions. To this purpose, we recommand to use a lower grid spacing value (e.g. 0.3) associated to a lower padding value (e.g. 0.2).

Path Finding¶

Epock can detect if a path exists between two pockets. It implements an A* (A star) algorithm. A* is complete and will always find a solution if one exists.

For more informations about this algorithm, see http://en.wikipedia.org/wiki/A*_search_algorithm