Analytical method¶

We implemented a simple program based on Epock’ source code in which a dummy pocket of known volume is hard coded, allowing to check Epock’s ability to return the reference volume when varying grid_spacing and precision.

Epock displays a limited number of input parameters has provided by Epock configuration files. Beside the MER, the two major parameters that can dramatically affect Epock performances are the grid_spacing and the precision parameters.

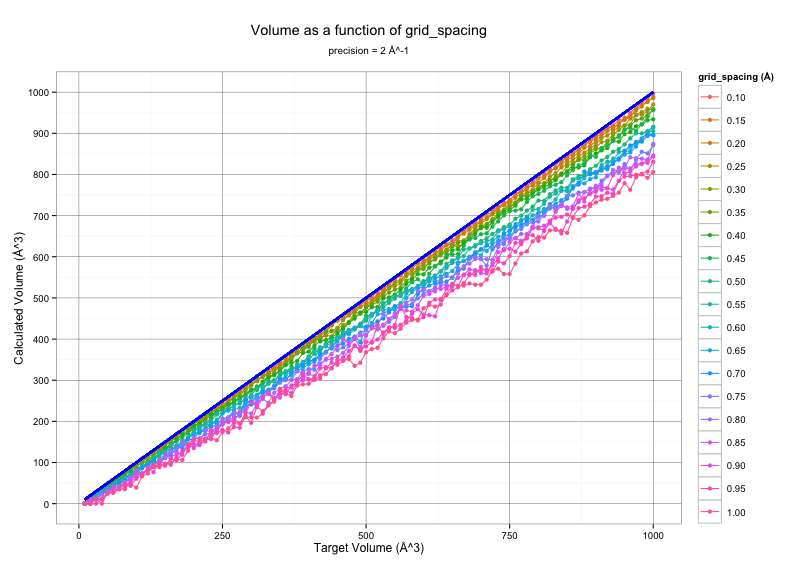
Influence of grid_spacing¶

The graph below shows Epock output volume for several input pocket volumes with a precision of 2 Å^-1 and various grid_spacing values. The target volume is shown as a thick blue line.

Influence of the grid_spacing parameter on the volume calculation: raw data.

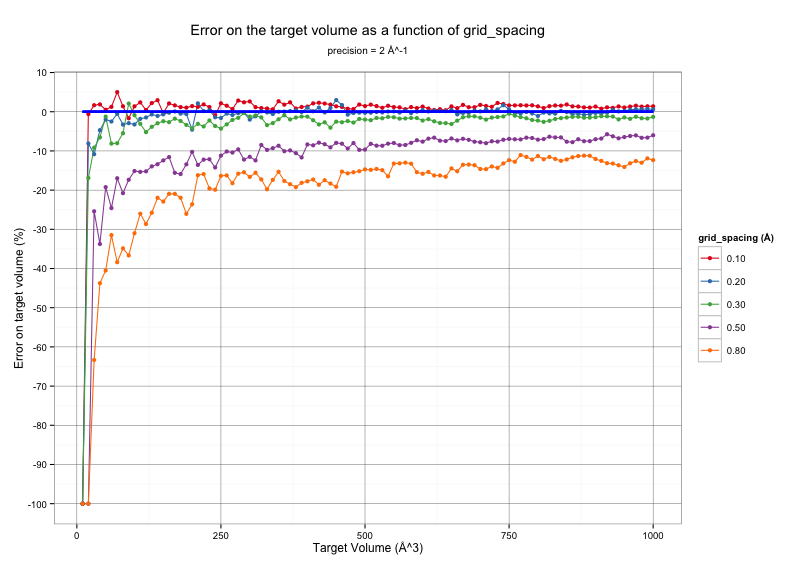
The same data can be represented as the percentage of error made on the volume calculation.

Influence of the grid_spacing parameter on the volume calculation: percentage of error.

As depicted from the figure above, the volume calculated by Epock largely depends on the grid spacing used for free space detection. Notably, Epock shows difficulties to accurately calculate very small volumes, i.e. < 50 Å^3. Such volumes correspond to sphere radii lower than 2.3 Å, which, in a biological context, depicts a very small cavity in which a water molecule would barely fit.

We recommand choosing a grid_spacing of 0.5 Å for a good compromise between accuracy and velocity.

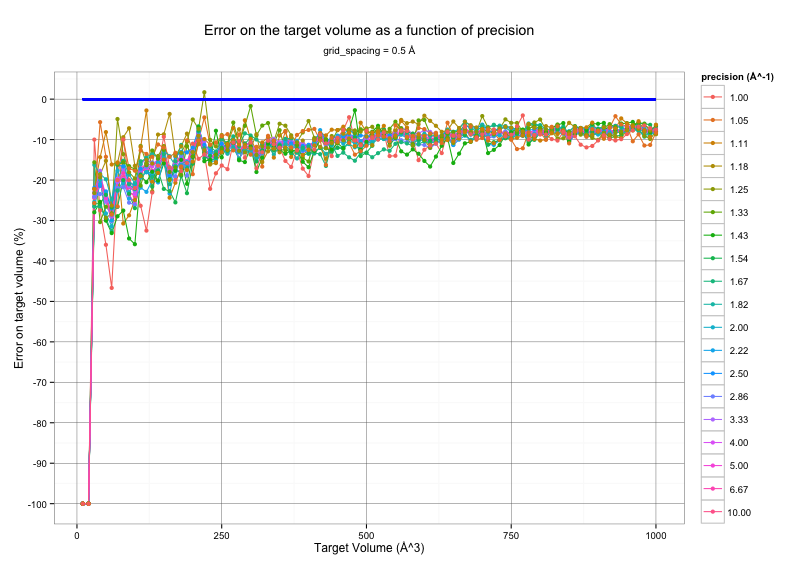
Influence of precision¶

The graph below shows Epock output volume for several input pocket volumes with a grid_spacing of 0.5 Å and various precision values. The target volume is shown as a thick blue line.

Influence of the precision parameter on the volume calculation: raw data.

The same data can be represented as the percentage of error made on the volume calculation.

Influence of the precision parameter on the volume calculation: percentage of error.

The figure above suggest that Epock output volume will barely depend on the value of the precision parameter.

We recommand choosing a precision of 2.0 Å^-1 for a good compromise between accuracy and velocity.

Non-analytical method¶

We created a system made of very close dummy atoms (recognized by Epock as carbon atoms) that form a box. All atoms within a given radius of the center of the box have been removed, resulting in a system that contains a “hole” of known volume in its center.

The material used to calculate the non-analytical error is public and available in the Epock benchmark package .

The two figures below show that Epock’s error on a pseudo-system is comparable to the analytical solution presented above.

Influence of the grid_spacing parameter on the volume calculation: raw data.

Influence of the grid_spacing parameter on the volume calculation: percentage of error.

Conclusion¶

We propose here to ways to assess Epock’s error on pocket of knwon volumes. Epock displays relatively low error with both methods.

For a good compromise between accuracy and velocity, we recommand using grid_spacing = 0.5 and precision = 2.0. In the test case presented here, i.e. the case of a perfect hard coded sphere of known volume, these settings cause Epock to underestimate the actual pocket volume of about 10 %.

However, it is quite difficult to predict the error Epock makes on a real protein pockets as their various bshapes are most probably far for a perfect sphere. As both the free space detected and the volume calculation depends on a grid, the result will also depend on the grid alignment that can hardly be customized. There is however no a priori reason to believe that Epock’s error would be more important on a protein pocket than on our test case.

From a general point a view, it is very important to visually check how well the free space detected by Epock fits the pocket (see the free space visual inspection section).